Quadratic Inequality
Definition
A quadratic inequality in two variables is any inequality that can be put into one of the following forms:
- y ≤ ax2 + bx + c (a ≠ 0).
- y < ax2 + bx + c (a ≠ 0).
- y ≠ ax2 + bx + c (a ≠ 0).
- y > ax2 + bx + c (a ≠ 0).
- y ≥ ax2 + bx + c (a ≠ 0).
A quadratic inequality in one variable is any inequality that can be put into one of the following forms:
- 0 ≤ ax2 + bx + c (a ≠ 0).
- 0 < ax2 + bx + c (a ≠ 0).
- 0 ≠ ax2 + bx + c (a ≠ 0).
- 0 > ax2 + bx + c (a ≠ 0).
- 0 ≥ ax2 + bx + c (a ≠ 0).
Recall that inequalities involving "<", "≠" and ">", are called strict inequalities, while inequalities involving "≤" or "≥" are not.
Example One - Quadratic Inequality in Two Variables
PROBLEM
Graph y > x2 - 4x + 3
SOLUTION
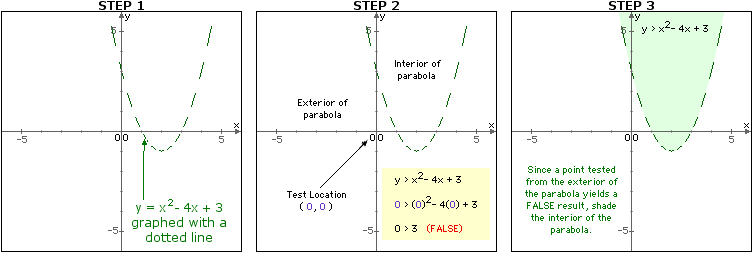
Step 1
If the inequality is strict, graph y = x2 - 4x + 3 using a dotted line, otherwise graph it using a solid line. Click here to see the steps.
Step 2
Choose a "test" location that is not part of the graph of the equality y = x2 - 4x + 3. If the origin is not part of the graph of the equality, it is a "good" location to choose. Substitute the values associated with the test location into the inequality.
y > x2 - 4x + 3 Substitute ( 0, 0 ) into the quadratic inequality
(0) > (0)2 - 4(0) + 3 Simplify
0 > 3 (FALSE)
Step 3
If the result is true, shade the region containing the test location. If the result is false, shade the region that does NOT contain the test location. Since ( 0, 0 ) yields a FALSE result, and ( 0, 0 ) is in the exterior of the parabola, the interior of the parabola is shaded.
Example Two - Quadratic Inequality in One Variable
PROBLEM
Solve and graph x2 + 2x - 8 ≤ 0
SOLUTION
Method One: Graph the corresponding quadratic inequality in two variables x2 + 2x - 8 ≤ y [or y ≥ x2 + 2x - 8]
Method Two: Solve x2 + 2x - 8 = 0 , then select appropriate test values for substitution into x2 + 2x - 8 ≤ 0
Method Three: Solve x2 + 2x - 8 ≤ 0 algebraically.
Example Three - Quadratic Inequality in One Variable
PROBLEM
Solve and graph x2 - 4x + 1 > 0
SOLUTION
Method One: Graph the corresponding quadratic inequality in two variables x2 - 4x + 1 > y [or y < x2 - 4x + 1]
Method Two: Solve x2 - 4x + 1 = 0 , then select appropriate test values for substitution into x2 - 4x + 1 > 0
Method Three: Solve x2 - 4x + 1 > 0 algebraically.
Demonstration
The applet will graph all of the inequalities described in the definition as well as the corresponding quadratic function y = ax2 + bx + c (a ≠ 0).
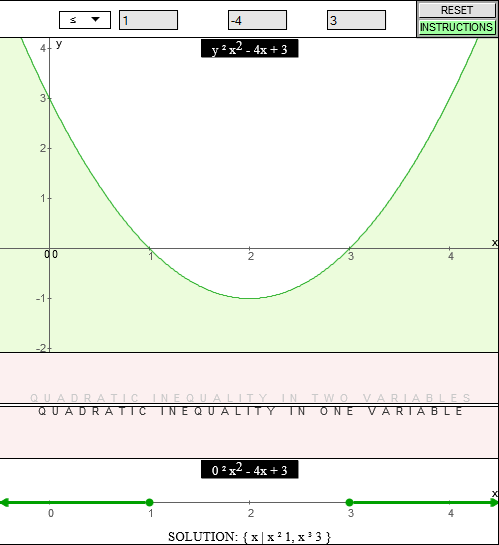 Image onlyInstructions text as in global.js
Image onlyInstructions text as in global.js